jueves, 20 de diciembre de 2012

Masa y peso :

Antes de que entremos en el tema de la gravedad y como actua, es importante entender la diferencia entre masa y peso.

Muchas veces usamos los terminos "masa" y "peso" como sinónimos en nuestro hablar diario, pero despues de leer esto te darás cuenta que son cosas completamente diferentes. La masa de un cuerpo es una medida de cuanta materia contiene. Un objeto con masa tiene una cualidad llamada inercia. si sacudes un objeto como una piedra en tu mano, te daras cuenta que requiere un empuje para empezar a moverse, y otro empuje para detenerse de nuevo. si la piedra esta inmovil, quiere quedarse inmovil. una vez que esta en movimiento, quiere seguir moviendose. Esta cualidad de la materia es su inercia. La masa tambien es una medida de cuanta inercia puede generar un objeto.

Peso es una cosa completamente distinta. Cualquier objeto en el universo con masa, atrae a cualquier otro objeto en el universo con masa. La fuerza de atraccion depende del tamaño, la masa y de que tan lejos esten el uno del otro. Para objetos de uso diario, esta atraccion gravitacional es muy pequeña, pero la atraccion entre un objeto muy grande, como la Tierra, y otro objeto, como tu, puede ser facilmente medido. Como? Solo hay que pararse en una pesa. Las pesas miden la fuerza de atraccion entre la tierra y tu. Esta fuerza de atraccion entre tu y la tierra (o cualquier otro planeta) se llama tu peso.

Si estas en una nave espacial, lejos de los planetas y pones una pesa debajo tuyo, la pesa leeria cero. Tu peso es cero. No tienes peso. Hay una linterna flotando cerca tuyo. tampoco tiene peso. Significa eso que tu y la linterna no tienen masa? Absolutamente no. si tomaras la linterna y la agitaras, tendrias que empujar para que empesara a moverse, y empujar de nuevo para que se detuviera. todavia tiene inercia, y por consiguiente, masa, aunque no tiene peso.

lunes, 10 de diciembre de 2012

Ley de gravitación universal

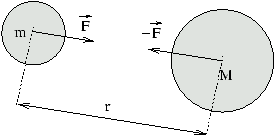
Fuerzas mutua de atracción entre dos esferas de diferente tamaño. De acuerdo con la mecánica newtoniana las dos fuerzas son iguales en módulo, pero de sentido contrario; al estar aplicadas en diferentes cuerpos no se anulan y su efecto combinado no altera la posición del centro de gravedad conjunto de ambas esferas.

La ley de la Gravitación Universal es una ley física clásica que describe la interacción gravitatoria entre distintos cuerpos con masa. Ésta fue presentada por Isaac Newton en su libro Philosophiae Naturalis Principia Mathematica, publicado en 1687, donde establece por primera vez una relación cuantitativa (deducida empíricamente de la observación) de la fuerza con que se atraen dos objetos con masa. Así, Newton dedujo que la fuerza con que se atraen dos cuerpos de diferente masa únicamente depende del valor de sus masas y del cuadrado de la distancia que los separa. También se observa que dicha fuerza actúa de tal forma que es como si toda la masa de cada uno de los cuerpos estuviese concentrada únicamente en su centro, es decir, es como si dichos objetos fuesen únicamente un punto, lo cual permite reducir enormemente la complejidad de las interacciones entre cuerpos complejos.
Así, con todo esto resulta que la ley de la Gravitación Universal predice que la fuerza ejercida entre dos cuerpos de masas $m_{1}$ y $m_{2}$ separados una distancia $r$ es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:

(1) $F = G \frac {m_{1}m_{2}} {r^2}$

donde

$F\,$ es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.

$G\,$ es la constante de la Gravitación Universal.

TERCERA LEY DE NEWTON

Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.

La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.

Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.

Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.

Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos.

SEGUNDA LEY DE NEWTON

La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.

La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:

F = m a

Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:

F = m a

La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s², o sea,

1 N = 1 Kg · 1 m/s²

La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m · a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.

Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

p = m · v

La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg·m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:

La Fuerza que actua sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,

F = dp/dt

De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para el caso de que la masa sea constante, recordando la definición de cantidad de movimiento y que como se deriva un producto tenemos:

F = d(m·v)/dt = m·dv/dt + dm/dt ·v

Como la masa es constante

dm/dt = 0

y recordando la definición de aceleración, nos queda

F = m a

tal y como habiamos visto anteriormente.

Otra consecuencia de expresar la Segunda ley de Newton usando la cantidad de movimiento es lo que se conoce como Principio de conservación de la cantidad de movimiento. Si la fuerza total que actua sobre un cuerpo es cero, la Segunda ley de Newton nos dice que:

0 = dp/dt

es decir, que la derivada de la cantidad de movimiento con respecto al tiempo es cero. Esto significa que la cantidad de movimiento debe ser constante en el tiempo (la derivada de una constante es cero). Esto es el Principio de conservación de la cantidad de movimiento: si la fuerza total que actua sobre un cuerpo es nula, la cantidad de movimiento del cuerpo permanece constante en el tiempo.